This function solves the problem of assigning customers (with demands) to centers (with capacities), so
total load is within the capacity and cost of travel is minimized for all customers.
Cost is defined through a matrix, which can be calculated by TCalc.Matrix2, TCalc.MatrixDyn2 or on your own.
Normally you will have many more customers than centers.
Demand should be a much smaller number than capacity. Otherwise the algorithm isn't very good at finding a solution.
Optimum results can only be achieved if demand is the same value for all customers. Such as 1.
If Demand parameter is nil (not set), the algorithm assumes 1 for all customers.
The function returns the cost of the solution.
The heuristics parameter can take three values, 1, 2 and 3. With method 1 you will typically get the lowest
overall cost values, while method 2 gives "nicer" looking solutions, but requires more time to get the solution.
We recommend trying both and pick the result you prefer.
Method 3 give similar results as method 2, but requires demand=1 (or nil) for all customers. It is ~5 times faster.
Property |
Dimension |
Capacity |
No of Centers |
Demand |
No of Customers |
Matrix |
No of Centers x Customers |
Assignment (output) |
No of Customers |
Load (output) |
No of Centers |
Unassigned |
No of unassigned customers |
Sample calculation time (demand = 1 for all customers, random center capacity, but sufficient in total):
Customers |
No of centers |
Calculation time - heuristic 1 |
Heuristic 2 |
100 |
10 |
16 ms |
16 ms |
1000 |
10 |
719 ms |
734 ms |
1000 |
100 |
1109 ms |
860 ms |
5000 |
10 |
220 sec (~ 4 minutes) |
19 sec |
5000 |
100 |
169 sec (~ 3 minutes) |
240 sec (4 min) |
5000 |
1000 |
15 sec |
3754 sec (62 min) |
Syntax: District(heuristic: integer): TCost;
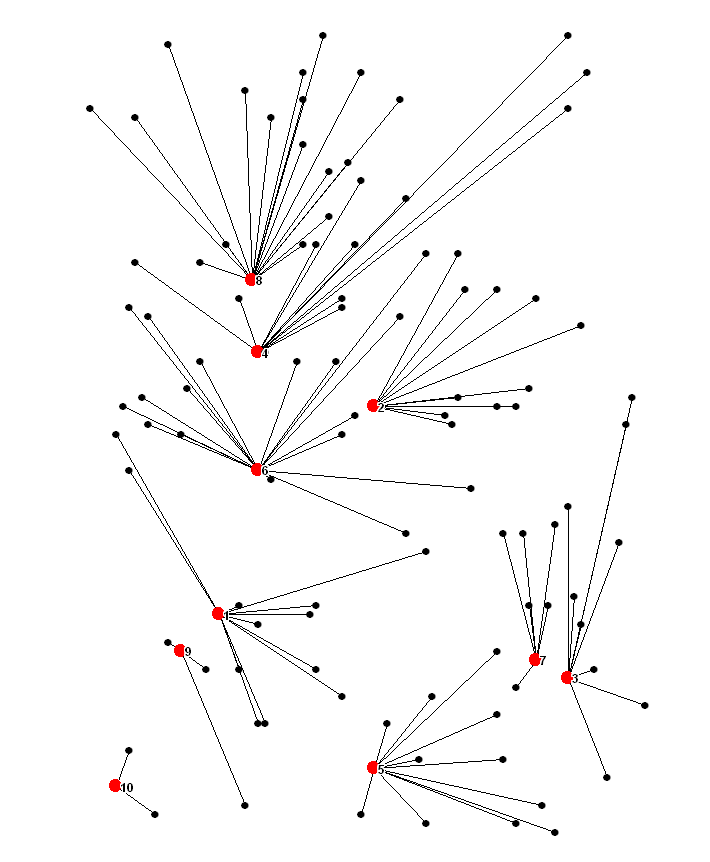
This is an example with 100 customers, assigned to 10 centers with varying capacity.
Customers and centers are connected with lines to make the result easier to view: